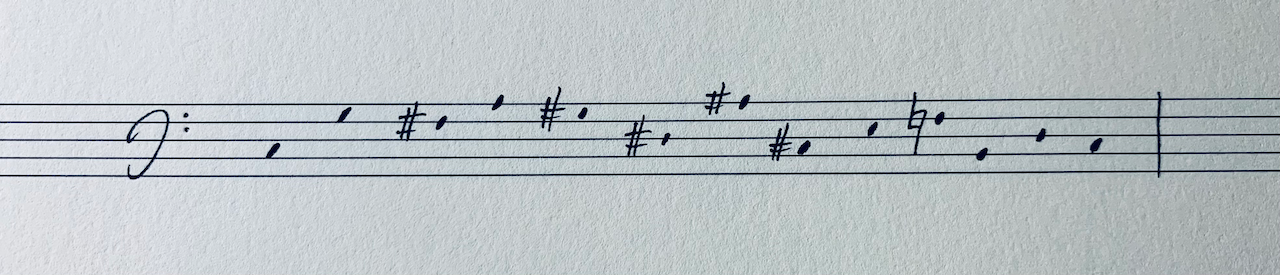The Musical Intervals
Intervals are units of music that happen on the smallest level.
The musical intervals are commonly thought of as the distance between two notes. Notes by themselves are not music, the smallest unit of music is the interval. Melodies are built with them. Harmonies are delivered to us in time through the intervals. The intervals seem to connect sound with its concrete and mathematical origins to our inner world of feeling—and thank goodness.
The intervals are a basic element of music, and their importance shouldn't be overlooked. Working with the fundamental intervals refines and nurtures our direct connection to our musicality. As this article aims to show, the intervals are the first opportunity that we have to experience a musical unity.
Basic foundations: What are the intervals?
Let's set the foundation by discussing the intervals as the "distances" between two tones. The distances can be measured between two notes on a staff or on an instrument. Counting the number of notes between the two notes that you are measuring (including the first note) is the first way to find and learn the musical intervals.
The easiest way of learning them is to look at an ascending major scale.
Figure 1. The diatonic C major scale, built from major and minor seconds.
The distance between the tonic (note 1) and the second note in the scale is a second, and the distance between the tonic and the fourth note of the scale is a fourth, and so on. The chromatic scale contains all 12 notes, and provides all of the possible intervals within an octave.
Figure 2. The 12 possible intervals have labels that indicate their size (the distance expressed as number) and their quality (M for major, m for minor, and P for perfect). M3 is read as "major third," m6 is read as "minor sixth," and P4 is read as "perfect fourth." T.T. is the tritone.
1. Figure 2 shows the musical intervals within one octave. The 12 intervals are outlined as increasing in size between each successive note of the ascending chromatic scale and the tonic, C. If you can, go ahead and sing or imagine each of the intervals and hear what they sound like.
2. Each of the intervals have a quality. Fifths, fourths, and octaves can be described as perfect. The seconds, thirds, sixths, and sevenths can be described as either major or minor. Typically major intervals are larger than minor intervals by 1 half step.
3. The intervals can be inverted by raising the lower note up by one octave.
4. Intervals also have directions. You can play them going up, or down.
Figure 3. Inverting each of the intervals in Figure 1 is done by raising the lower note one octave, and shows a new pattern of intervals, revealing a symmetry.
Octave inversions of intervals always add up to 9. For example, the inversion of a 3rd is a 6th. Inversion of a 2nd is a 7th, and inversion of a 4th is a 5th. Major intervals become minor when inverted, and when inverted minor intervals become major. Perfect intervals remain perfect when they are inverted.
Figure 4. Series 2 from Paul Hindemith's Craft of Musical Composition
Figure 4 shows the 12 intervals arranged in a much more useful way. The intervals in this series are arranged based on the same order that they appear in the harmonic series: first the octave, then the fifth, followed by the fourth, the major third, the minor third, the major second, and so on.
It reveals a remarkable pattern: 5 pairs of intervals and their inversions—fifths and fourths, major thirds and minor sixths, minor thirds and major sixths, major seconds and minor sevenths, minor seconds and major sevenths—flanked by the octave and the tritone.
Even if you don't understand this fully yet, keep reading on. I hope to introduce an approach that will let you access the significance of the intervals. Knowledge of this full theory will come with time. Since intervals are what builds scales, melodies, chords, and is the basic unit of musical construction, how can we develop our relationship with them?
Hear all that goes on when you sing an interval.
Figure 5. A minor third up.
What is it like to sing an interval? What does singing one reveal?
Try this out. Sing a minor third.
The first thing that I hear is the stability of the first tone. While singing the first note, I have to imagine the next tone in my head. I almost have to hear the second note inside the sound of the first note. Now, I move to the second note.
When I sing the second tone, I am moved by a whole bunch of sensations. For me, I think of Batman (thanks, Hans Zimmer) and I'm also moved emotionally. Why? How does this happen? The reason that these associations arise is that while I am singing the second tone I am still connected to the first tone.
Consider the following. I sing one note. Then take a break. Then I come back. And sing the second note. I've already forgotten how the first note felt. There is no meaning. No connection, no association.
But when I actually connect the two notes and live the relationship between them, the interval arises.
Try it! Pay attention to the inner hearing of the second note of the interval that is being sung before you actually move to the second note.
If you manage to do that, then you have successfully lived an interval. It feels good, doesn't it!
By listening to the interval and letting it arouse our inner sensations, the body allows us to appreciate what nature has built into sound.
An interval is a process of how one tone becomes another.
It's not true that each time I sing an interval, I live it. When I'm walking down the street humming a tune, it's very easy for that to remain an unconscious singing of several notes that go together. Even trained musicians play entire concerts of notes in succession without connecting them. Living an interval is an act that requires your full consciousness. Imagine how different it would be if you hear a performance and the violinist delivers each interval in the piece as they are within her. Imagine what that music would sound like.
An interval is a process that takes place in space and in time. As you experienced, a key part of singing an interval is the transition from one note to another. It takes place in the mind of the musician. We have to hear the second tone before we sing it to live the connection.
Intervals are the smallest musical unities.
Figure 6. A major sixth down.
The intervals are the connections of two notes, and they happen inside of the musician. The same feeling that exists inside of an interval is the thing that binds together the disparate structures of an entire musical form. You can say that this connection is the "glue" that holds music together. And what is that glue made of? Nothing that we can point to in the physical world. The vibrations of two tones may exist as a fact of reality but your consciousness is the location where they actually find relations with themselves.
Singing an interval is the first opportunity for us to experience a musical unity.
Okay. What does that mean?
In simplest terms, we want to live the interval as one thing. Let's say we are playing the interval between C and G. You can analyze the spectra of sound inside each of them and that's fine. But it really becomes music when the musician lives the 2 two notes and traverses them, making it one experience that has a beginning, middle and end. And of course, the same can be true about an entire piece of music.
Figure 7. Ascending perfect fourths separated by a minor second.
Intervals have impacts and resolutions. Each interval has a root.
As we discovered, the stability of sound gives rise to all of the characteristics and effects that make music possible. When you sing an interval, which of the two notes is more stable?
As you continue to sing them, you'll eventually find that for certain intervals it is clear that the first note is more stable. It might seem obvious, after all the first note has the benefit of being the first musical impact on the ear.
Figure 8. Fifths and fourths to study, which of the two tones is more stable?
But it's not always that the first note is more stable. Sometimes, the second note is more impactful.
The clearest example of this is the fifths in Figure 7. When you sing the first interval from C to G, listen closely to find which is more stable. It's the C, isn't it? Now sing the second interval from C to F.
The F sounds like it has more weight, and our ears actually hear the F as the more stable of the two. The second note is more stable than the first. As we saw the intervals can be inverted, so a perfect fifth going down will lead to the same note one octave higher as a perfect fourth going up. When we sing C to F ascending (bar 3 of Figure 8) we also hear that F is more stable than the C, even though it's higher. Try singing C to Ab, a descending major 3rd. Which of the two is more stable?
Practice singing each of the 12 possible intervals both up and down and try to find which of the two is more stable. This research can be thought of as finding the root of the interval. The acoustical theory behind the intervallic roots actually comes from combination tones. When you play 2 sounds in perfect tune with each other, a 3rd sound emerges and it's audible and real (meaning it's not just perceived or imaginary. You can measure the third vibration with a scientific instrument). Two sopranos singing an E and a higher C (a minor sixth) in perfect tune will hear a bass G tone. The laws of music have their basis in the laws of sound.
So each interval has a natural tendency. Familiarize yourself with the intervals because it is the stuff of music. Then when you are composing you can go with or against the natural tendency to create musical tension.
The Three Dimensions
Before moving on to a brief commentary on the intervals to guide your practice, I think it's important to introduce some vocabulary that will be useful in describing how our inner life is moved by the musical forces in an interval. These dimensions describe the musical tension—the "glue" that holds music together—that emerges when you are touched by an interval. These dimensions can be thought of as degrees of less or more.
Dimension of more or less consonance and dissonance.
Certain combinations of tones are more harmonious than others. This can be intuited and explained based on the fact that each note has a family of overtones that will clash against another note. Figure 4 is a very useful way of organizing the intervals in the order from more consonant to more dissonant.
Dimension of more or less introversion and extroversion.
Extroverted intervals seem to move the spirit to expand outward. Introverted intervals seem to move the spirit more in an inward direction. Certain intervals are very clearly one or the other, and others are more indeterminate. Compare a major sixth ascending and a minor sixth ascending (for example, from C to higher A, and C to higher Ab). Which is more extroverted? I hear the minor sixth as more introverted. Compare a major and minor third descending (G to lower E, and G to lower Eb). Which third do you hear as more extroverted? There really is no right answer here, this dimension is beyond logic, but it is real.
Dimension of more or less frequency.
Pretty self explanatory, intervals can either go up or down. The direction that the intervals go plays a huge role in the way that they move us. I sincerely invite you to begin researching and mapping the intervals in this way, to see what you find. It will be encouraging to share with others who are looking for the same.
“We shall not do as the ancients did, and carry over earthly relations to happenings far out in space. Rather, we shall observe in the finest building unit of music the play of the same forces that rule the movements of the most distant nebulae. ”
Getting to know them: Commentary on the Intervals
The Octave
The great organizer of scales. We all feel that the upper note of an octave is the "higher image" of the lower. The octave is the first interval that appears in the harmonic series, producing a pure double of the fundamental frequency.
Fifths and Fourths
When we look at fifths and fourths, we are looking at the notes that are closest to the fundamental. When played together the two notes that form this interval are extremely harmonious. The fifth is very much a part of the fundamental due to the closeness of the note in the overtone series.
An ascending fifth has a similar effect as a descending fourth. When we hear it in a melody, our ears immediately lock into the more stable tone. The ascending fifth (and descending fourth) has a strong extroverted quality due to its dominant (V) nature. The descending fifth (and ascending fourth) has a strong introverted quality due to the subdominant (IV) nature.
“Man feels transported in the fifth. He enters into his own being in the fourth.”
One excerpt that came to mind is the first movement of Debussy's Nocturnes. The Bb in the bass introduces a further lower fifth, creating an introverted expanse.
Figure 9. Debussy's Nuages. You can see in the first violins (the second and third staff from the top) the rich series of fifths that help create his unique sound world.
Thirds and Sixths
Thirds and sixths are quite harmonious and melodic, and their meaning really depends on the context that they are in. Our entire traditional system of harmony is based on chords that are built with thirds.
Seconds and Sevenths
Seconds and sevenths are the most melodic intervals. Scales are built with combinations of major and minor seconds.
The Tritone
The tritone is often introduced as the most dissonant interval, but learning how to use them is extremely beneficial. It has a striking effect on the ear, being the combination of two notes that are the furthest away from each other. When we hear the tritone it has a strong tendency to resolve in the following ways.
Figure 9. The same tritone has the tendency to resolve in two ways, which can quickly open the doors to new harmonic possibilities.
Figure 10. Words and Music Tom Kelly and Billy Steinberg
The tritone isn't always dissonant, it can also be extremely melodic. Whitney Houston traces a tritone from G to C# in the bridge of the hit classic So Emotional, and we love her for it.
Intervals in Melodic Analysis
Figure 11. The melodies in the Rite of Spring are pretty simple.
Figure 12. Sing or play these pitches. How do each of the intervals contribute to the overall phrase?
You can analyze any music that may seem complicated at first by simply analyzing the intervals.
Even a score as complicated as the Rite of Spring is just a collection of vertical and horizontal intervals, and can be approached through their analysis.
Figure 13. Melodies are built from intervals. Each one contributes to the overall line of musical tension.
To summarize, the intervals are more than just the distances between 2 notes. They are the transformation of one tone into another. When you start to combine intervals, you build chords. As soon as we have more than 3 tones, we've left the discussion of intervals and have moved to the world of chords and harmony, and that's exactly what we'll do on Day 5.
The best exercise that will strengthen your connection to the intervals: The 12 Tone Row
The exercise is to arrange the 12 notes of the chromatic scale in a tone row that begins and ends with the same pitch. The goal is to use each of the 12 notes only once, to stay within one octave, and to arrange them in a way that guides the ear from beginning to end. The practice is to discover the smoothest way to use each to guide the ear away from the starting note and eventually return home to the starting note in one satisfying motion.
Try one out for yourself! Tomorrow I'll share a ton of examples for you to learn from to start incorporating this exercise into your practice. When you do compose one, share them with me at jordan@jordanali.com.
Figure 14. Example of a 12 tone row exercise.